# 树(Tree)
二叉树中的节点最多只能有两个子节点:一个是左侧子节点,另一个是右侧子节点。这个定义有助于我们写出更高效地在树中插入、查找和删除节点的算法。二叉树在计算机科学中的应用非常广泛。
# 二叉搜索树(BST)
二叉搜索树(BST)是二叉树的一种,但是只允许你在左侧节点存储(比父节点)小的值,在右侧节点存储(比父节点)大的值。
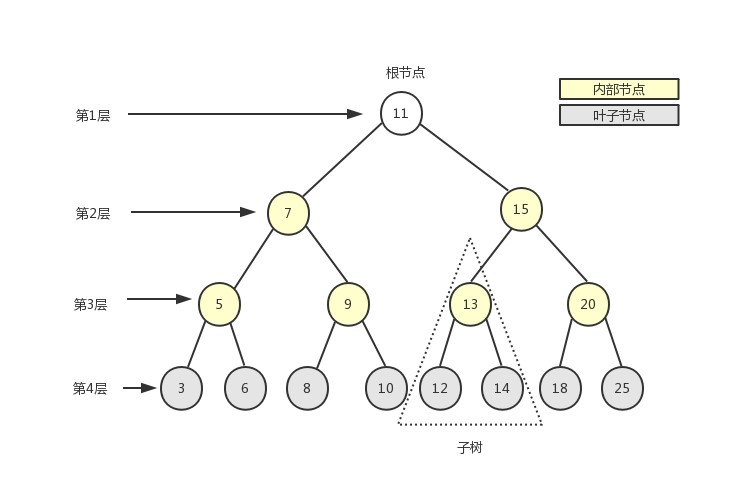
这棵树中最多有两个分支, 因此是二叉树。
根节点: 一棵树最顶部的节点内部节点: 在它上面还有其它内部节点或者叶节点的节点叶节点: 处于一棵树根部的节点子树: 由树中的内部节点和叶节点组成
首先就要定义一个Node类,用于存放树的节点,其构造与前面的链表类似。
// 节点定义
function Node(key) {
this.key = key
this.left = null;
this.right = null;
}
添加新节点
顶点为空则直接在该处插入, 若不为空, 则通过比较顶点的 key 和插入元素的 key 判断该插入到顶点的左侧还是右侧,后面进行如上递归
function BinarySearchTree() {
let root = null;
// 插入
this.insert = (key) => {
const node = new Node(key)
if (root == null) { // 设值当前节点为根节点
root = node
} else {
insertNode(root, node)
}
function insertNode(parent, node) {
if (parent.key > node.key) { // 当前节点大于新节点,则新节点放左边
if (parent.left === null) { // 若为空,则直接赋值为新节点, 出栈
parent.left = node
} else {
insertNode(parent.left, node) // 依次从根节点递归
}
} else if (parent.key < node.key) { // 当前节点小于新节点,则新节点放右边
if (parent.right === null) {
parent.right = node
} else {
insertNode(parent.right, node)
}
}
}
return root
}
}
const tree = new BinarySearchTree()
tree.insert(23)
tree.insert(45)
tree.insert(16)
tree.insert(37)
tree.insert(3)
tree.insert(99)
tree.insert(22)
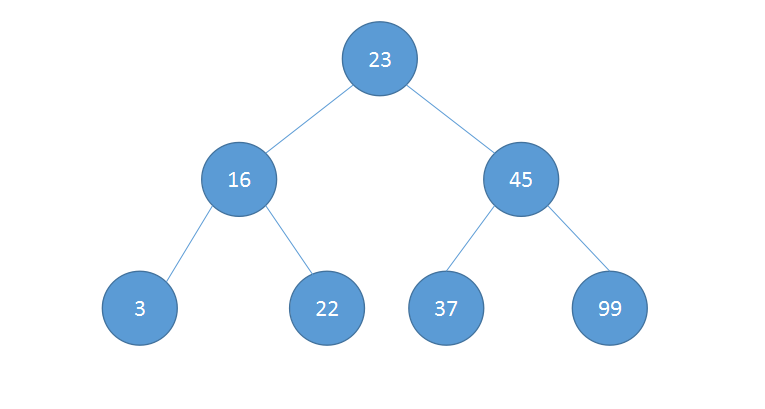
上述插入数据后,会形成如下的二叉树
# 树的遍历
# 中序
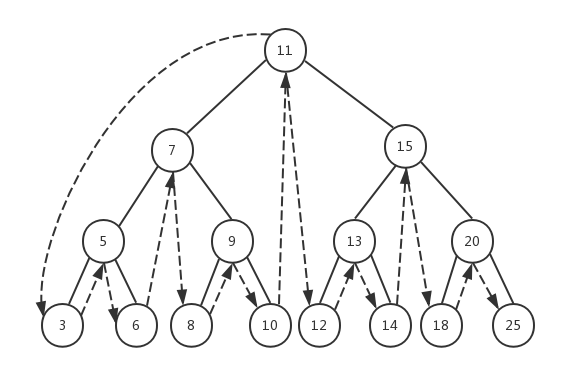
中序遍历是一种以上行顺序访问BST所有节点的遍历方式,也就是以从最小到最大的顺序访问所有节点
中序遍历使用递归的方式最容易实现。该方法需要以升序访问树中所有节点,先访问左子树,再访问根节点,最后访问右子树
// 中序遍历
this.inOrder = (cb) => {
inOrder(root, cb)
function inOrder(node, cb) {
if (node) {
inOrder(node.left, cb)
cb(node.key)
inOrder(node.right, cb)
}
}
}
中序遍历结果如下:
let str = ''
let p = (val) => str += val + ' '
tree.inOrder(p)
console.log(str)
// 3 16 22 23 37 45 99
# 先序
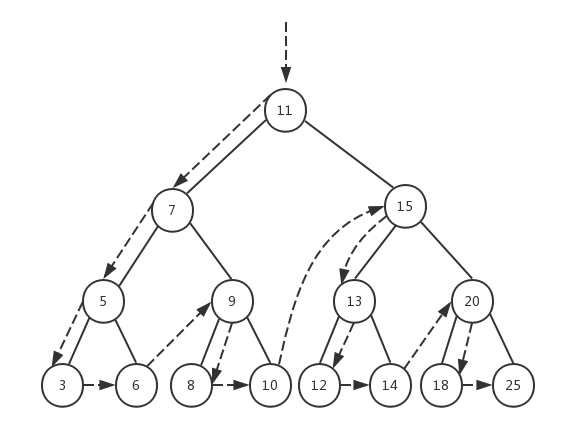
先序遍历是以优先于后代节点的顺序访问每个节点的。
先序遍历和中序遍历的不同点是:先序遍历会先访问节点本身(1),然后再访问它的左侧子节点(2),最后是右侧子节点(3),而中序遍历的执行顺序是:{2}、{1}和{3}。
// 先序遍历
this.preOrder = (cb) => {
preOrder(root, cb)
function preOrder(node, cb) {
if (node) {
cb(node.key)
preOrder(node.left, cb)
preOrder(node.right, cb)
}
}
}
先序遍历结果如下:
tree.preOrder(p)
// 23 16 3 22 45 37 99
# 后序
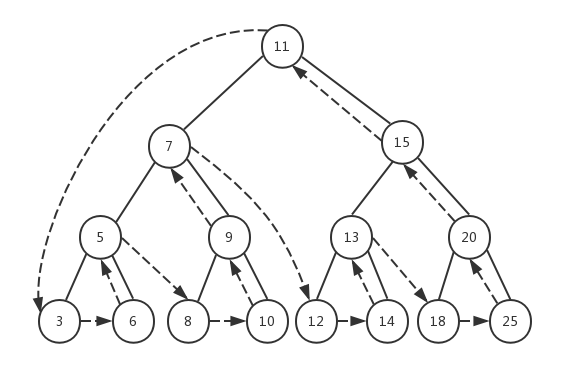
后序遍历会先访问左侧子节点(1),然后是右侧子节点(2),最后是父节点本身(3)。
你会发现,中序、先序和后序遍历的实现方式是很相似的,唯一不同的是行1、2和3的执行顺序。
// 后序遍历
this.postOrder = (cb) => {
postOrder(root, cb)
function postOrder(node, cb) {
if (node) {
postOrder(node.left, cb)
postOrder(node.right, cb)
cb(node.key)
}
}
}
后序遍历结果如下:
tree.postOrder(p)
// 3 22 16 37 99 45 23
# 查找运算
# 最大值&最小值
遍历右子树,直到右子树的某个节点的 right 为 null 时,该节点保存的即为最大值
遍历左子树,直到左子树的某个节点的 left 为 null 时,该节点保存的即为最小值
// 最大值:最右边
this.max = (node = root) => {
let current = node
while (current && current.right) {
current = current.right
}
return current.key
}
// 最小值:最左边
this.min = (node = root) => {
let current = node
while (current && current.left) {
current = current.left
}
return current.key
}
# 指定值
根据上面添加新节点可得知:当前节点小于新节点,则新节点放右边,反之放左边
查找的时候,根据key值进行判断,该往左右还是右边循环
// 查找指定值
this.search = (key) => {
if (root == null) {
return null
}
let current = root
while (current) {
if (current.key === key) {
return current
} else if (current.key < key) {
current = current.right
} else {
current = current.left
}
}
}
console.log(tree.search(100)) // Node {key: 100, left: Node, right: null}
console.log(tree.search(111)) // undefined
# 删除节点
从BST上删除节点的操作最复杂,其复杂程度取决于删除哪个节点。
如果删除没有子节点的节点,那么非常简单。
如果节点只有一个子节点,不管是左子节点还是右子节点,就变得稍微有点复杂了。
删除包含两个子节点的节点最复杂。
this.remove = (key) => {
const removeNode = (node, key) => {
if (node == null) return null
if (key == node.key) {
if (node.left == null && node.right == null) { // 没有子节点
node = null
return node
}
else if (node.left == null) { // 有右子节点
node = node.right
return node
}
else if (node.right == null) { // 有左子节点
node = right.left
return node
}
// 包含两个子节点
let min = this.min(node.right)
node.key = min.key
node.right = removeNode(node.right, min.key)
return node
} else if (key < node.key) { // 小于节点,往左边
node.left = removeNode(node.left, key)
return node
} else { // 大于节点,往右
node.right = removeNode(node.right, key)
return node
}
}
removeNode(root, key)
}
首先要找到树中待删除的节点,这需要进行递归遍历,从根节点开始
如果key值小于当前节点的值,则遍历左子树,如果key值大于当前节点的值,则遍历右子树。
注意,在递归遍历的过程中,我们将node(这里的node传入的是树的根节点)的left指针或right指针逐级指向下一级节点,然后返回整个node。
当找到要删除的节点后,我们要处理三种情况:
// 先赋值 与图片一致的树
tree.insert(11);
tree.insert(7);
tree.insert(15);
tree.insert(5);
tree.insert(9);
tree.insert(13);
tree.insert(20);
tree.insert(3);
tree.insert(6);
tree.insert(8);
tree.insert(10);
tree.insert(12);
tree.insert(14);
tree.insert(18);
tree.insert(25);
# 没有子节点
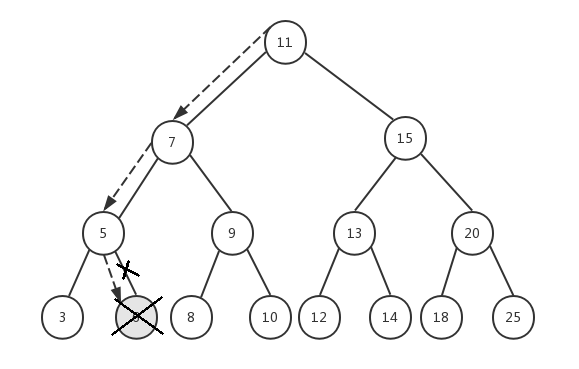
假设我们要删除节点6,传入根节点11,整个执行过程如下:
- node=11,key=6,6<11,递归执行
removeNode(7, 6) - node=7,key=6,6<7,递归执行
removeNode(5, 6) - node=5,key=6,6>5,递归执行
removeNode(6, 6) - node=6,key=6,6=6,并且节点6的
left和right都为null, 所以我们将节点6设置为null,并且返回null - 递归返回到步骤3,节点5的
right将获取步骤4的返回值null - 递归返回到步骤2,节点7的
left依然指向节点5,保持不变 - 递归返回到步骤1,节点11的
left依然指向节点7,保持不变 - 最后返回节点11
# 一个子节点
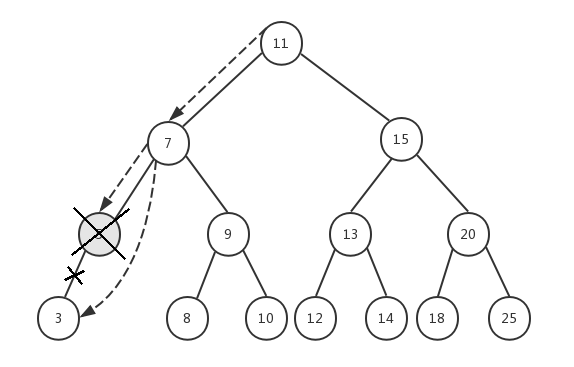
前面已经删除了节点6,假设我们现在要删除节点5,它有一个左子节点3,我们依然传入根节点11,来看看整个执行过程:
- node=11,key=5,5<11,递归执行
removeNode(7, 5) - node=7,key=5,5<7,递归执行
removeNode(5, 5) - node=5,key=5,5=5,并且节点5的
left=3,right=null,所以我们将节点5替换成它的左子节点3,并返回节点3 - 递归返回到步骤2,节点7的
right将获取步骤3的返回值3 - 递归返回到步骤1,节点11的
left依然指向节点7,保持不变 - 最后返回节点11
# 左右子节点
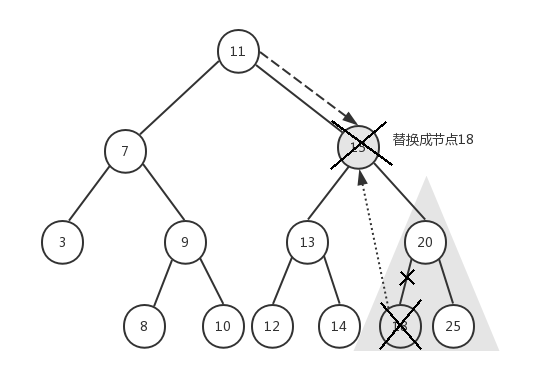
前面已经删除了节点6和节点5,现在我们要删除节点15,它有左右子树,我们传入根节点11,来看下具体执行过程:
- node=11,key=15,15>11,递归执行
removeNode(15, 15) - node=15,key=15,15=15
- 进入包含两个子节点的判断条件里
- 此时我们需要找到节点15的右子树中的
最小节点18 - 将节点15的key替换成节点18的key
- 将节点15的
right节点(即节点20)作为起始节点进行遍历,找到并删除节点18 - 最后再将节点15(此时它的key是18)的
right指针指向节点20,并返回节点15
- 递归返回到步骤1,节点11的
right依然指向节点15,但此时节点15的key已经变成18了 - 最后返回节点11
OK
解决上面右子树的最小节点的疑问, 为什么要找到这个最小节点呢??
试想一下,当删除节点15之后,为了保证我们的二叉搜索树结构稳定,必须用节点15的右子树中的最小节点来替换节点15,如果直接将11的next指向20,则20将会有三个子节点13、18、25,这显然已经不符合我们二叉树的定义了。如果将节点25用来替换节点15,节点20的值比节点25的值小,不应该出现在右子节点,这也不符合我们的二叉搜索树的定义。
所以,只有按照上述过程才能既保证不破坏树的结构,又能删除节点。
注: (右子节点的最小值 or 左子节点的最大值) 两则皆可, 任选其一, 神奇的二叉树
# 自平衡树
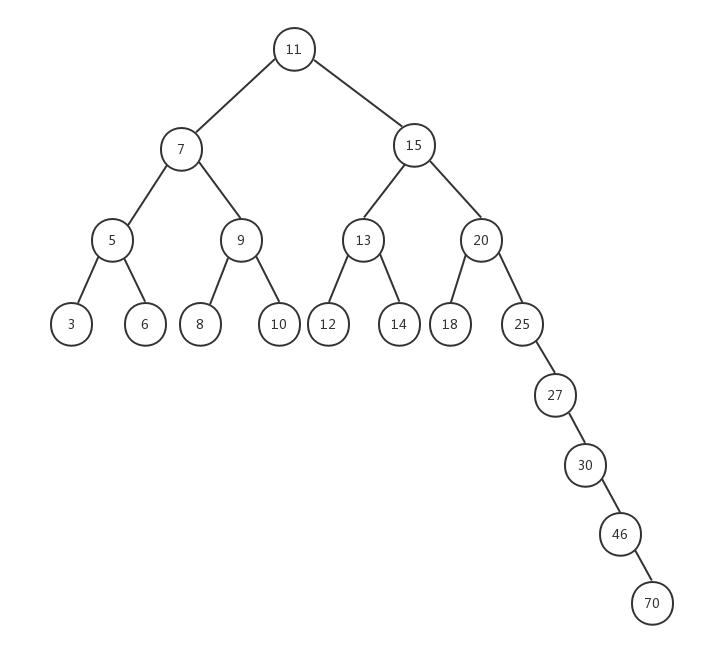
上面的BST树(二叉搜索树)存在一个问题,树的一条边可能会非常深,而其它边却只有几层,这会在这条很深的分支上添加、移除和搜索节点时引起一些性能问题。
如下图所示:
class AVLTree extends BinarySearchTree {
constructor() {
super()
}
// LL旋转: 向右旋转
rotationLL(node) {
let tmp = node.left
node.left = tmp.right
tmp.right = node
return tmp
}
// RR旋转: 向左旋转
rotationRR(node) {
let tmp = node.right;
node.right = tmp.left;
tmp.left = node;
return tmp;
}
// LR旋转: 先向左旋转,然后再向右旋转
rotationLR(node) {
node.left = this.rotationRR(node.left);
return this.rotationLL(node);
}
// RL旋转: 先向右旋转,然后再向左旋转
rotationRL(node) {
node.right = this.rotationLL(node.right);
return this.rotationRR(node);
}
getNodeHeight(node = this.root) {
if (node == null) {
return 0
} else {
let left = this.getNodeHeight(node.left)
let right = this.getNodeHeight(node.right)
return Math.max(left, right) + 1
}
}
insertNode(key) {
this.insert(key)
// 左子树高度大于右子树高度
if (this.getNodeHeight(this.root.left) - this.getNodeHeight(this.root.right) > 1) {
if (key < this.root.left.element) {
this.root = this.rotationLL(this.root)
} else {
this.root = this.rotationLR(this.root)
}
}
// 右子树高度大于左子树高度
else if (this.getNodeHeight(this.root.right) - this.getNodeHeight(this.root.left) > 1) {
if (key > this.root.right.element) {
this.root = this.rotationRR(this.root)
} else {
this.root = this.rotationRL(this.root)
}
}
}
removeNode(key) {
this.remove(key)
// 左子树高度大于右子树高度
if (this.getNodeHeight(this.root.left) - this.getNodeHeight(this.root.right) > 1) {
if (key < this.root.left.element) {
this.root = this.rotationLL(this.root)
} else {
this.root = this.rotationLR(this.root)
}
}
// 右子树高度大于左子树高度
else if (this.getNodeHeight(this.root.right) - this.getNodeHeight(this.root.left) > 1) {
if (key > this.root.right.element) {
this.root = this.rotationRR(this.root)
} else {
this.root = this.rotationRL(this.root)
}
}
}
}
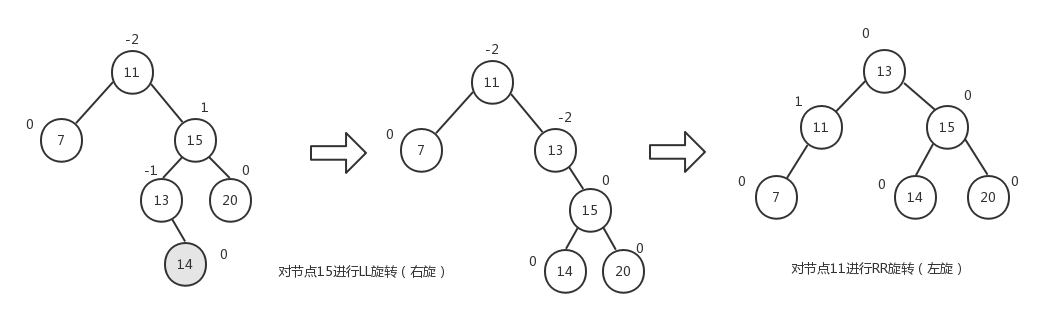
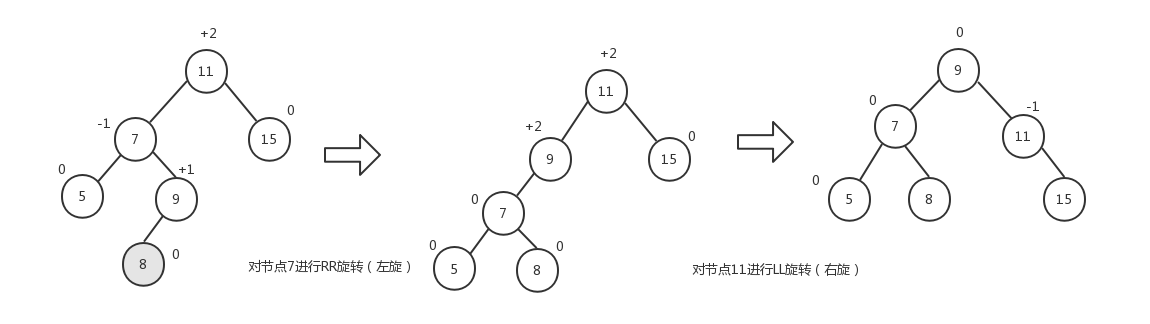
对于LL旋转和RR旋转,我们可以按照上面的示意图来看下执行过程。
LL旋转,node=11,node.prev是7,所以tmp=7。然后将node.prev指向tmp.next,即将11的prev指向9。接着将tmp.next指向node,即将7的next指向11。即完成了图中所示的旋转。
RR旋转,node=11,node.next是15,所以tmp=15。然后将node.next指向tmp.prev,即将11的next指向13。接着将tmp.prev指向node,即将15的prev指向11。即完成了图中所示的旋转。
const trees = new AVLTree()
trees.insertNode(11);
trees.insertNode(7);
trees.insertNode(15);
trees.insertNode(5);
trees.insertNode(9);
trees.insertNode(8);
trees.preOrder((value) => console.log(value));
// 9 7 5 8 11 15
LR旋转是RR旋转和LL旋转的组合:
const trees = new AVLTree()
trees.insertNode(11);
trees.insertNode(7);
trees.insertNode(15);
trees.insertNode(13);
trees.insertNode(20);
trees.insertNode(14);
trees.preOrder((value) => console.log(value));
// 13 11 7 15 14 20
RL旋转是LL旋转和RR旋转的组合: